东昌中学高中二年级期末数学试题
2020.01
1、 填空题
1. 关于
、
的方程组
的增广矩阵为__________
2. 若
（
是虚数单位），则
__________
3. 已知
，
，则
在上的投影是__________
4. 行列式
中，第2行第1列元素的代数余子式的值为__________
5. 设椭圆的一个焦点为，且
，则椭圆的规范方程为__________
6. 已知直线与平行，则
的值是__________
7. 若向量、
的夹角为150°，
，
，则__________
8. 已知圆
，则过圆上点
的切线方程是 __________
9. 下列命题：（1）
，，则
；（2），则不成立；（3），则
是纯虚数；（4），，则
；（5），则；其中正确的命题有__________个
10. 设
、
分别是双曲线
的左、右焦点，若点
在双曲线上，且
，则__________
11. 为抛物线
上一动点，
为的焦点，
为抛物线内部一点，则
的最小值为__________
12. 已知关于的方程
有两个不一样的解，则实数的取值范围是__________
2、 选择题
13. 已知复数
，
（为虚数单位），在复平面内
对应的点在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
14. 已知点
，
，向量
，则向量
（ ）
A. 
B. 
C. 
D.
15. “直线与抛物线的相切”是“直线与抛物线仅有一个公共点”的（ ）条件
A. 充分非必要 B. 必要非充分 C. 充要 D. 非充分非必要
16. 双曲线
绕坐标原点
逆时针旋转
后可以成为函数
的图像，则的
角度可以为（ ）
A. 30° B. 45° C. 60° D. 90°
3、 解答卷
17. 设
，关于的方程
的两个根分别是和.
（1）当
时，求与
、的值；
（2）当
，
时，求的值.
18. 已知
，，
，（）.
（1）若，且∥，求的值；
（2）若，且，求的取值范围.
19. 已知关于、的方程，表示圆.
（1）求的取值范围；
（2）若该圆与直线相交于
、两点，且，求实数的值.
20. 已知抛物线：（）.
（1）若上一点
到其焦点的距离为3，求的方程；
（2）若，斜率为2的直线交于两点、，交轴的正半轴于点，为坐标原点，，求点的坐标.
21. 概念：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特点三角形”，
假如两个椭圆的“特点三角形”是一样的，则称这两个椭圆是“相似椭圆”，并将三角形的
相似比称为椭圆的相似比，已知椭圆.
（1）若椭圆
，判断与
是不是相似？假如相似，求出与的相似比，
假如不相似，请说明理由；
（2）写出与椭圆相似且焦点在轴上，短半轴为
的椭圆
的规范方程，若在椭圆
上存在两点、关于直线对称，求实数的取值范围；
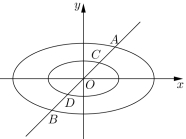（3）如图：直线与两个“相似椭圆”和
（
，
）分别交于点、和点、
，试在椭圆和椭圆上分
别作出点和点（非椭圆顶点），使△和△
组成以为相似比的两个相似三
角形，写出具体作法.（不必证明）
参考答案
1、 填空题
1. 
2. 
3. 4.
5. 6. 
或5 7. 8.
9. 10. 11. 
12.
2、 选择题
13. B 14. A 15. A 16. C
3、 解答卷
17.（1），
，；（2）.
18.（1）；（2）.
19.（1）；（2）
.
20.（1）；（2）
.
21.（1）相似，相似比为2；（2）（），
；（3）作法：过原
点作直线（），交椭圆与椭圆于点和点，则△和△即为所求相似三角形，且相似比为.
